Diagonal Sum In Binary Tree| diagonal sum in Binary Tree Problem Solution

 diagonal sum in Binary Tree Problem Solution -

In this blog we will see How to print Diagonal Sum In Binary Tree| diagonal sum in Binary Tree Problem Solution . It is most common question related to recursion lets read diagonal sum in Binary Tree Problem.

Problem Statement-

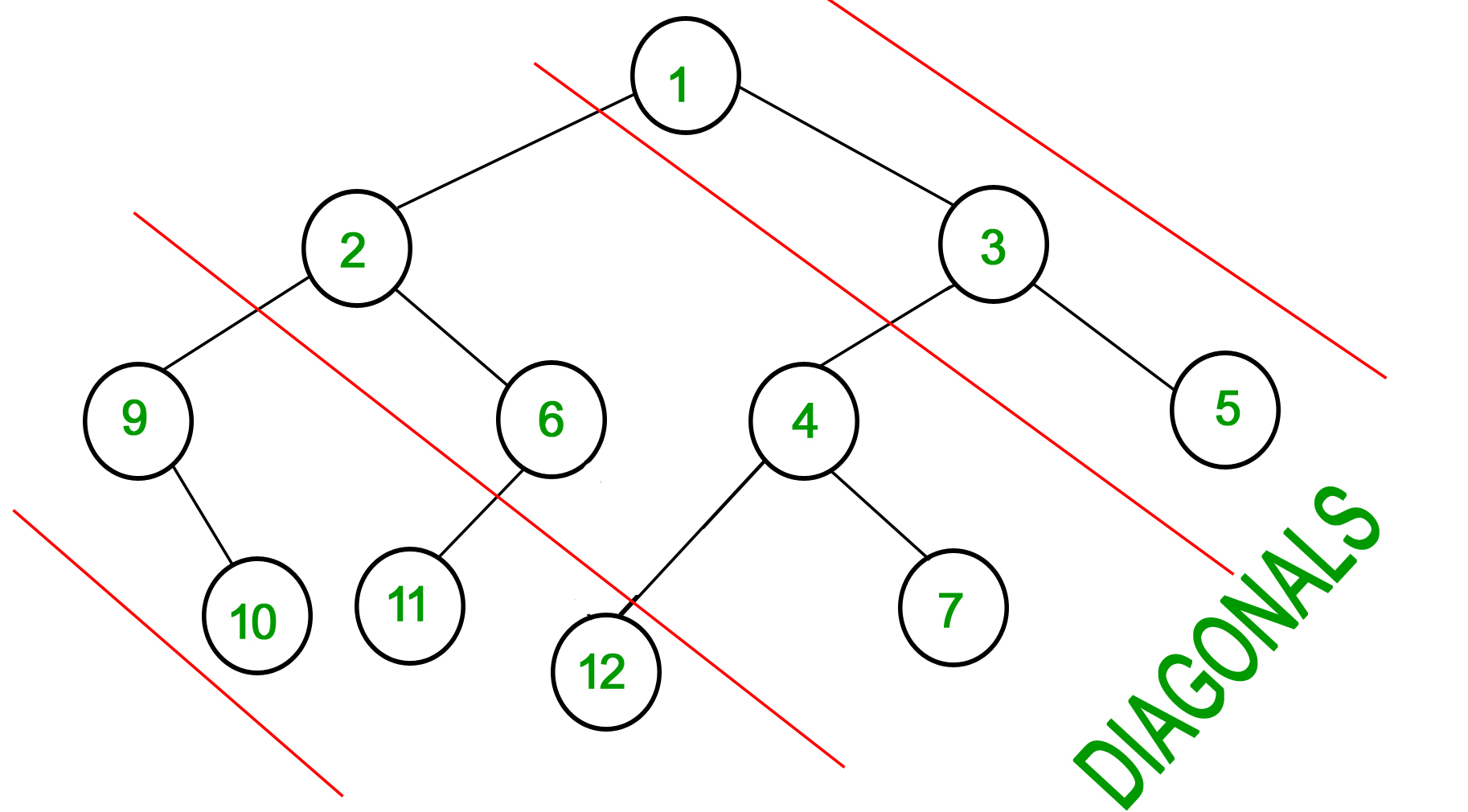
Consider Red lines of slope -1 passing between nodes (in following diagram). The diagonal sum in a binary tree is the sum of all node’s data lying between these lines. Given a Binary Tree of size N, print all diagonal sums.

For the following input tree, output should be 9, 19, 42.
9 is sum of 1, 3 and 5.
19 is sum of 2, 6, 4 and 7.
42 is sum of 9, 10, 11 and 12.

Example 1:

Input:
         4
       /   \
      1     3
           /
          3
Output: 7 4 

Example 2:

Input:
           10
         /    \
        8      2
       / \    /
      3   5  2
Output: 12 15 3 

Your Task:
You don't need to take input. Just complete the function diagonalSum() that takes root node of the tree as parameter and returns an array containing the diagonal sums for every diagonal present in the tree with slope -1.

Expected Time Complexity: O(N).
Expected Auxiliary Space: O(N).

Constraints:
1<=Number of nodes<=105

Note: The Input/Ouput format and Example given are used for system's internal purpose, and should be used by a user for Expected Output only. As it is a function problem, hence a user should not read any input from stdin/console. The task is to complete the function specified, and not to write the full code.

Problem Credit - GeeksForGeeks (This Problem is taken From geeks for geeks website).

Recommended: Please try your approach before moving on to the solution.

Let's Jump To my Solution now-

After a deep observation, I divided this binary tree having n diagonal and I will write a function that will calculate all diagonal sum and store solution in a map.

for example, diagonal number 1 ans will be stored in a map having key 1.

see the image below

Fucntion Descreption ->

I have written a function that returns the sum of diagonal if I pass the current root, map(for storing diagonal sum till now ), and diagonal number to this function parameter. This is a magical function, isn't it 😆😆  XD. 

Now I have to find the smallest possible case which will help me to write base case of my problem 

if the root doesn't exist I have to simply return because the tree is empty.

Now I found the smallest problem  Lets write base case.

 if(!root){

        return ;

    }

Now How to write the next block of code.

Think like that -

I don't know the solution but if somehow i get diagonal sum excluded root node my task  will be minimized and i will  add only root node to previous sum.

`At the same time, I noticed that whenever I go to the left of my root node every time my diagonal number increased by 1. By Using this Property I can write my diagonal sum in Binary Tree Problem Solution.

so Let's write the induction step now if you think like that it will very easy to write induction step-

calculateDiagonalSum(diagonalNumber+1,root->left,mymap);

     calculateDiagonalSum(diagonalNumber,root->right,mymap);

     mymap[diagonalNumber]+=root->data;

     return ;

    Hopefully, You understood the entire solution if not comment below.

Here is the complete code of my solution -